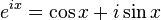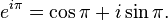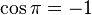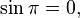삼각함수와 지수함수에 대한 관계를 나타낸다. 오일러의 등식은 이 공식의 특수한 경우이다.
오일러의 공식은 가장 아름다운 것들을 포함하고 있다. 세가지 기본적 산술연산: 덧셈, 곱셈, 지수를 포함하고 있으며 다섯가지의 가장 기본적인 상수: 0, 1, pi, theta, i 를 포함하고 있다.

The identity is a special case of Euler's formula fromcomplex analysis, which states that
for any real number x. (Note that the arguments to thetrigonometric functions sine and cosine are taken to be in radians, and not in degrees.) In particular, with x = π, or one half turn around the circle:
Since
and
it follows that
which gives the identity

The exponential function ez can be defined as the limit of(1 + z/N)N, as N approaches infinity, and thus eiπ is the limit of(1 +iπ/N)N. In this animation N takes various increasing values from 1 to 100. The computation of (1 + iπ/N)N is displayed as the combined effect of N repeated multiplications in the complex plane, with the final point being the actual value of (1 +iπ/N)N. It can be seen that as N gets larger (1 +iπ/N)N approaches a limit of −1.
http://en.wikipedia.org/wiki/Euler's_identity
http://ko.wikipedia.org/wiki/%EC%98%A4%EC%9D%BC%EB%9F%AC%EC%9D%98_%EA%B3%B5%EC%8B%9D
'자연 과학' 카테고리의 다른 글
| 조류 독감 H5N1 바이러스 virus 논란: 정보 유통의 정당성 및 감안해야 할 위험 (0) | 2011.12.29 |
|---|---|
| 태양의 코로나를 지나 살아나온! 혜성 러브조이 Comet Lovejoy! 예상치 못 한 굉장함 (0) | 2011.12.25 |
| higgs boson 힉스 보존 입자 존재하는가, 증명은 시간문제인가 (0) | 2011.12.16 |
| quark 분수의 전하를 가진 입자 쿼크 (0) | 2011.12.16 |
| Taylor Series 테일러 급수 문서 자료 및 동영상 강의 (0) | 2011.11.26 |